Métodos
Elige la distribución probabilística adecuada para tu simulación ztris con esta sencilla guía paso-a-paso que te ayudará a modelar mejor tu compañía
El Value Tree (o árbol de valoración) es una herramienta visual esencial para facilitar, capturar y compartir la estrategia y visión de una compañía.
Al construir el Value Tree de tu compañía, comenzamos por identificar el nodo principal que servirá de base para nuestro modelo, basándonos en nuestros objetivos estratégicos.
Este nodo principal, o nivel 0, puede variar según lo que queremos analizar:
Valoración de la compañía o maximización del valor de inversión: Utilizamos la compañía entera como nodo nivel 0.
Análisis de la rentabilidad desde necesidades de capital: Optamos por el flujo de caja como nodo principal.
Optimización de recursos: Podemos usar el ROI u otra medida similar como nivel 0.
Análisis de beneficio operativo: El EBITDA o similar podría ser el nodo principal.
Enfoque en ventas: Podemos centrarnos en esta métrica específica.
La estructura del Value Tree se define por nuestros objetivos, lo que requiere una clara definición de estos antes de comenzar el análisis.
3 sencillos pasos para la Construcción y Modelización en Ztris:
Define los objetivos del análisis: Determina qué aspectos de la empresa necesitas explorar y cuáles son tus metas finales.
Define las variables y sus relaciones: Establece cómo se relacionan las diferentes variables dentro de tu modelo.
Modeliza cada variable: Utiliza las distribuciones estadísticas adecuadas para simular el comportamiento de cada variable, lo cual detallamos a continuación.
Antes de sumergirnos en tipos específicos de distribuciones estadísticas, es crucial entender algunos conceptos clave que influirán en la elección de la distribución adecuada para cada situación:
Simetría vs. Asimetría:
- Simétricas: Las distribuciones simétricas tienen sus datos distribuidos de manera uniforme alrededor de la media. La distribución normal es un ejemplo clásico, útil cuando los datos no presentan sesgo y se acumulan cerca de un promedio central.
- Asimétricas: En las distribuciones asimétricas, los datos se inclinan hacia un lado, ya sea a la derecha (sesgo positivo) o a la izquierda (sesgo negativo). Ejemplos incluyen la distribución lognormal y la exponencial, ideales para modelar variables que no pueden ser negativas o que crecen exponencialmente.
Centrado y Posición de los Resultados Esperados:
- Centrado: Se refiere a distribuciones donde los datos se acumulan alrededor de un punto central, como la media o mediana. Este es un factor clave para prever resultados alrededor de un objetivo esperado.
- Posición de los Resultados: Algunas distribuciones, como la binomial o la geométrica, son útiles para modelar la probabilidad de ocurrencia de eventos específicos y sus resultados pueden indicar la probabilidad de lograr ciertos objetivos.
Variables Discretas vs. Continuas:
- Discretas: Las distribuciones discretas modelan variables que toman valores específicos y contables, como el número de ventas o incidentes. Ejemplos incluyen la distribución binomial y la geométrica.
- Continuas: Las distribuciones continuas son adecuadas para modelar variables que pueden tomar cualquier valor dentro de un rango, como el tiempo o el precio. Ejemplos son la distribución normal y la exponencial.
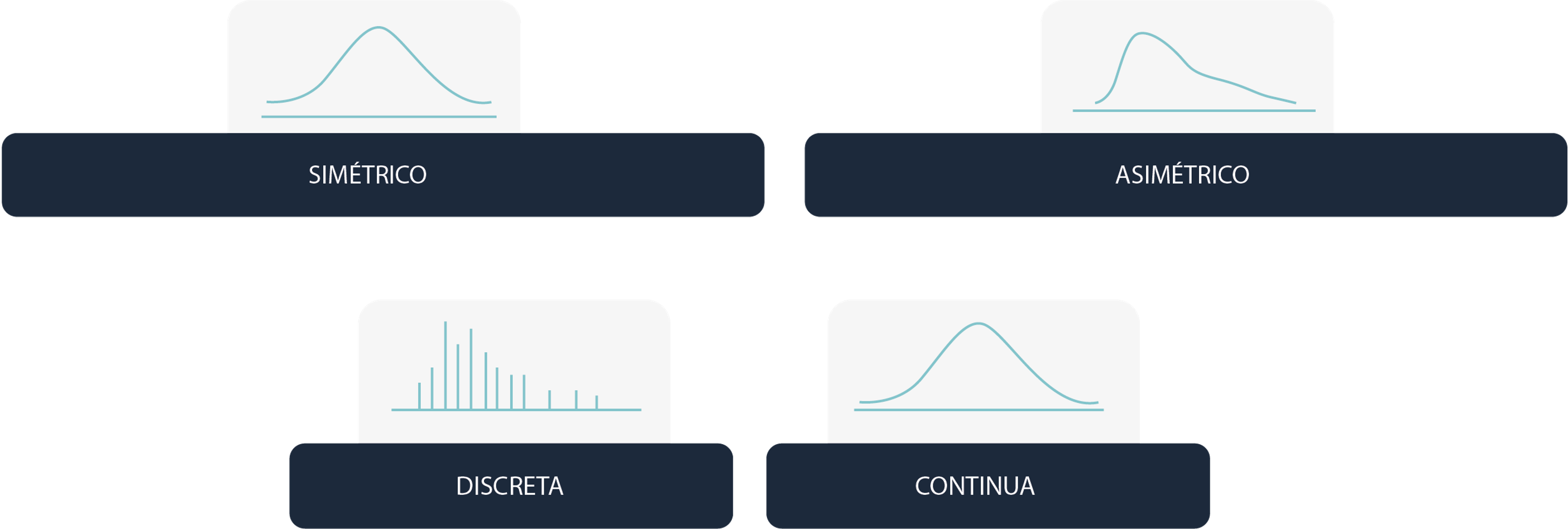

¿Cómo elegir la distribución adecuada para cada tipo de dato?
Comprender y aplicar correctamente estas doce distribuciones estadísticas permite a los usuarios de Ztris simular con precisión una amplia variedad de procesos y escenarios empresariales. Este enfoque no solo mejora la capacidad analítica, sino que también fortalece la toma de decisiones estratégicas a través de una visualización clara y datos modelados efectivamente.
Distribuciones Discretas
1. Binomial:
Aplicación: Útil para modelar el número de éxitos en una serie de ensayos binarios independientes.
Ejemplo: Determinar la probabilidad de lograr un número específico de ventas exitosas en un día.
2. Geométrica:
Aplicación: Modela el número de intentos necesarios para obtener el primer éxito en ensayos independientes.
Ejemplo: Estimar el número de llamadas necesarias para lograr la primera venta.
3. Binomial Negativa (Pascal):
Aplicación: Extiende la distribución geométrica para contar el número de intentos hasta alcanzar un número fijo de éxitos.
Ejemplo: Prever cuántas presentaciones de producto serán necesarias para alcanzar tres ventas.
4. Hipergeométrica:
Aplicación: Similar a la binomial pero en situaciones donde los ensayos no son independientes, como la selección sin reemplazo.
Ejemplo: Calcular la probabilidad de seleccionar un número específico de piezas defectuosas de un lote fijo.
5. Poisson:
Aplicación: Modela el número de eventos en un intervalo de tiempo fijo cuando estos eventos ocurren con una tasa constante e independientemente del tiempo transcurrido desde el último evento.
Ejemplo: Estimar el número de llamadas a un centro de atención al cliente en una hora.
Distribuciones Continuas
6. Normal:
Aplicación: Ideal para variables que se distribuyen de manera simétrica alrededor de la media, como errores de medición o características físicas.
Ejemplo: Modelar el error en las estimaciones de demanda.
7. Lognormal:
Aplicación: Usada para variables que no pueden ser negativas y tienen un potencial de crecimiento exponencial.
Ejemplo: Estimar el crecimiento del valor de activos financieros a lo largo del tiempo.
8. Exponencial:
Aplicación: Utilizada para modelar el tiempo entre eventos en un proceso Poisson.
Ejemplo: Calcular el tiempo promedio entre fallos de un equipo.
9. Gamma:
Aplicación: Extiende la distribución exponencial para modelar el tiempo hasta que ocurren varios eventos.
Ejemplo: Estimar el tiempo total necesario para completar múltiples tareas.
10. Beta:
Aplicación: Ideal para modelar variables que tienen un rango limitado, como porcentajes y proporciones.
Ejemplo: Prever el porcentaje de mercado que capturará un nuevo producto.
11. Triangular:
Aplicación: Útil para estimaciones basadas en un valor mínimo, máximo y más probable.
Ejemplo: Calcular el coste probable de un proyecto cuando se conoce el rango de coste posible.
12. Uniforme:
Aplicación: Adecuada cuando cualquier resultado dentro de un intervalo continuo es igualmente probable.
Ejemplo: Simular decisiones aleatorias o distribuciones de recursos uniformes.
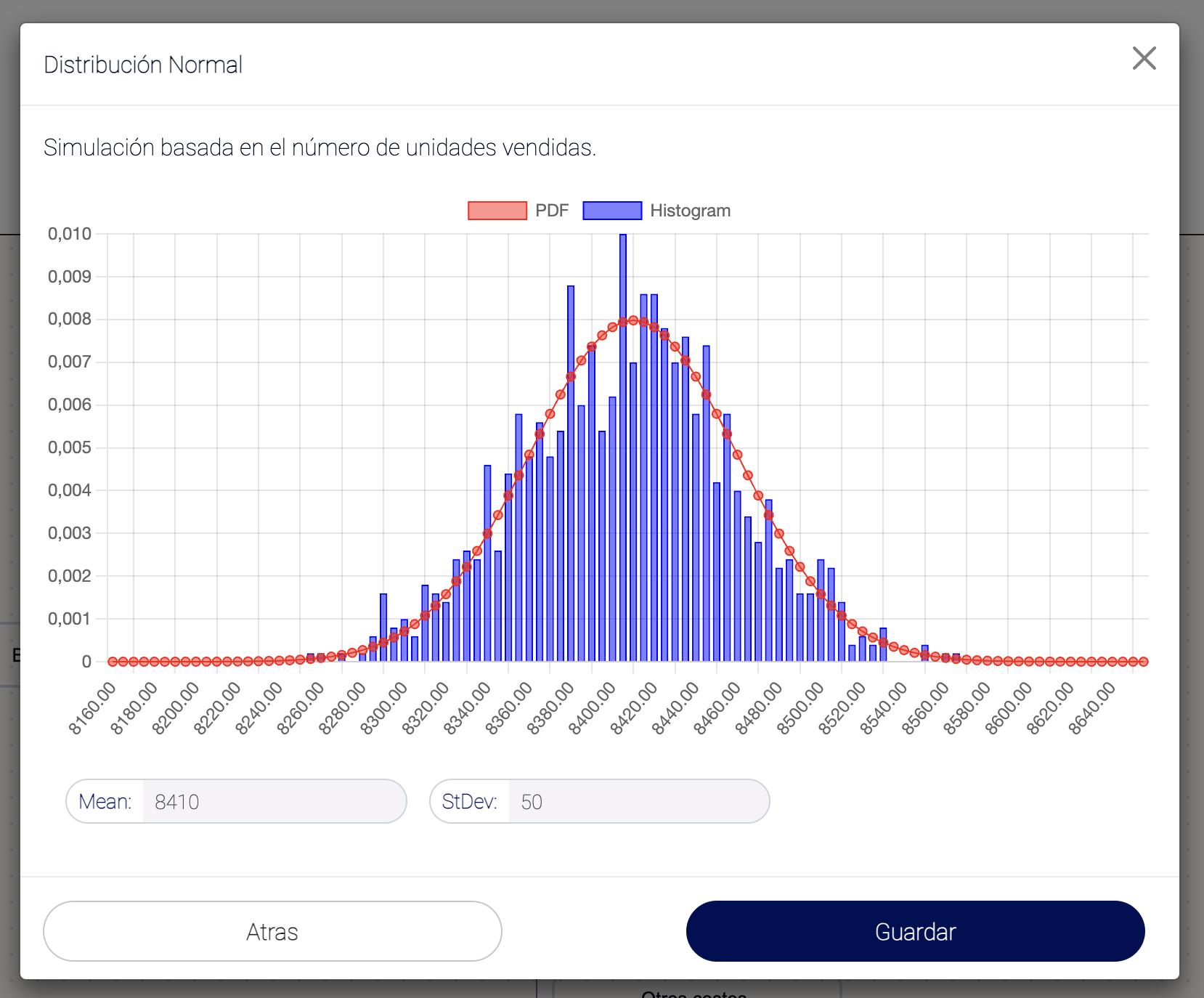
Y luego, ¿qué?
Una vez modeladas las variables, el siguiente paso es ejecutar la simulación y evaluar los resultados. Este análisis permitirá:
Validar la precisión del modelo: Comprobar si las simulaciones reflejan los resultados esperados o históricos.
Identificar áreas de mejora: Ajustar las distribuciones o parámetros basados en los resultados de la simulación.
Realizar análisis de sensibilidad: Entender cómo cambios en los inputs afectan los outputs, lo cual es crucial para la planificación estratégica y la toma de decisiones bajo incertidumbre.